- photo contests ▼
- photoshop contests ▼
- Tutorials ▼
- Social ▼Contact options
- Stats ▼Results and stats
- More ▼
- Help ▼Help and rules
- Login
Recursion – The Art and Ideas Behind M. C. Escher’s Drawings
M.C. Escher occupies a unique spot among the most popular artists of the past century.
While his contemporaries focused on breaking from traditional art and its emphasis on realism and beauty, Escher found his muse in symmetry and infinity.
His attachment to geometric forms made him one of modernism’s most recognizable artists and his work remains as relevant as ever.
 Escher’s early works are an odd mix of cubism and traditional woodcut. From these beginnings, one could already note Escher’s fondness for repetition and clean shapes. While simple and exploratory, these works were the signs of a nascent art career.
Escher’s early works are an odd mix of cubism and traditional woodcut. From these beginnings, one could already note Escher’s fondness for repetition and clean shapes. While simple and exploratory, these works were the signs of a nascent art career.
 Beginning in the mid-1930s, Escher’s work turned very pointedly to the style we associate with him today. Some of his most iconic works were completed in this period and his fascination with spherical distortion, recursion, and optical illusions took full force. Recursion figured very prominently in this and later periods, so it’s worth understanding what it is and how Escher was led to it.
Beginning in the mid-1930s, Escher’s work turned very pointedly to the style we associate with him today. Some of his most iconic works were completed in this period and his fascination with spherical distortion, recursion, and optical illusions took full force. Recursion figured very prominently in this and later periods, so it’s worth understanding what it is and how Escher was led to it.
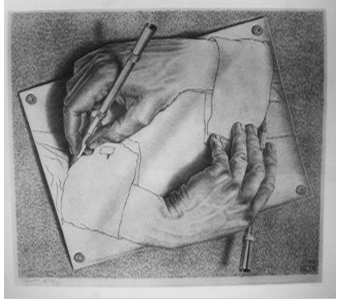 Recursion is a fairly simple concept. Something that recurs references itself. The reflection in a mirror of a mirror is recursive: the reflected mirror is reflecting its own image and doing so indefinitely. You’ve also likely seen the Droste effect when using camcorders hooked up to a TV or a computer: when the camcorder is looking at the screen, you can see an infinite series of screens generate themselves, since the camcorder is recording the same image that it’s sending to the screen. The game Portal is a great example of recursion, when two portals could be opened side by side in a narrow space and looking in either one produced an infinite series of the same image.
Recursion is a fairly simple concept. Something that recurs references itself. The reflection in a mirror of a mirror is recursive: the reflected mirror is reflecting its own image and doing so indefinitely. You’ve also likely seen the Droste effect when using camcorders hooked up to a TV or a computer: when the camcorder is looking at the screen, you can see an infinite series of screens generate themselves, since the camcorder is recording the same image that it’s sending to the screen. The game Portal is a great example of recursion, when two portals could be opened side by side in a narrow space and looking in either one produced an infinite series of the same image.
 Escher combined recursion and pattern repetition in a unique way. Some of the works featuring this combination exhibits some complex mathematical and physical ideas, but to the casual viewer the works are sublime. The swans image above features this sort of combination. Note that the swans are tiled very precisely, with the same distance from adjacent swans and swans in the next row. Note also that they are in a closed loop, one construct made possible with recursion.
Escher combined recursion and pattern repetition in a unique way. Some of the works featuring this combination exhibits some complex mathematical and physical ideas, but to the casual viewer the works are sublime. The swans image above features this sort of combination. Note that the swans are tiled very precisely, with the same distance from adjacent swans and swans in the next row. Note also that they are in a closed loop, one construct made possible with recursion.
 The above image is an example of the Mandelbrot set. The Mandelbrot set, along with other sets, is an example of a fractal. Fractals are fundamentally based on the idea of infinite recursion. If you zoom in to a particular spot in the fractal, you’ll perhaps see a different arrangement of patterns, but you would still be able to zoom in to any one of them forever. Though fractals became popularly understood (at least in the mathematical world) after Escher had completed the bulk of his work, some of Escher’s images exhibit the same traits seen in fractal sets.
The above image is an example of the Mandelbrot set. The Mandelbrot set, along with other sets, is an example of a fractal. Fractals are fundamentally based on the idea of infinite recursion. If you zoom in to a particular spot in the fractal, you’ll perhaps see a different arrangement of patterns, but you would still be able to zoom in to any one of them forever. Though fractals became popularly understood (at least in the mathematical world) after Escher had completed the bulk of his work, some of Escher’s images exhibit the same traits seen in fractal sets.

 Ascending and Descending, shown above, shows a particularly interesting perspective trick. To the casual observer, the people on the top ramp are ascending and descending the steps at the same time. Of course we can follow the steps ourselves and see that they ascend three-quarters of the way and descend and ascend at the same time on the right edge. These particular steps are curiously shallow, which allows the effect to work. It’s a simple, albeit effective optical illusion.
Ascending and Descending, shown above, shows a particularly interesting perspective trick. To the casual observer, the people on the top ramp are ascending and descending the steps at the same time. Of course we can follow the steps ourselves and see that they ascend three-quarters of the way and descend and ascend at the same time on the right edge. These particular steps are curiously shallow, which allows the effect to work. It’s a simple, albeit effective optical illusion.
 Print Gallery, above, exploits human vision once more. If we follow with our eyes the print the boy is looking at, we see that at a certain point, the buildings from the background come to the foreground and connect to the window panes that we were looking through before. The picture has a very prominent blank patch on it, however, where we surmise Escher had difficulties completing the pattern in the image. A mathematician named Henrik Lenstra has completed the image where the patch is and explained the mathematics behind Print Gallery as well.
Print Gallery, above, exploits human vision once more. If we follow with our eyes the print the boy is looking at, we see that at a certain point, the buildings from the background come to the foreground and connect to the window panes that we were looking through before. The picture has a very prominent blank patch on it, however, where we surmise Escher had difficulties completing the pattern in the image. A mathematician named Henrik Lenstra has completed the image where the patch is and explained the mathematics behind Print Gallery as well.
 Probably the most famous of Escher’s work, Relativity is the best example of Escher’s excursions into optical illusions, patterns, and recursion. The underlying pattern is best understood once we follow the figure on the very bottom to the middle of the image, Escher’s favorite place. We see three different planes and a number of people bound to the gravity of these planes. We suspect that at some point two people on different planes will cross each other, but this never happens in the image. Each plane is expertly extended beyond our field of vision. The animated version of this work shows how Relativity’s world works.
Probably the most famous of Escher’s work, Relativity is the best example of Escher’s excursions into optical illusions, patterns, and recursion. The underlying pattern is best understood once we follow the figure on the very bottom to the middle of the image, Escher’s favorite place. We see three different planes and a number of people bound to the gravity of these planes. We suspect that at some point two people on different planes will cross each other, but this never happens in the image. Each plane is expertly extended beyond our field of vision. The animated version of this work shows how Relativity’s world works.
Escher’s early works


Recursion
Few people have heard of Roger Penrose, H.S.M. Coxeter, or George Polya, but these mathematicians greatly influenced Escher’s approach to art. Penrose and Coxeter especially had a lasting impact on Escher and his mathematical research. Penrose was interested in repetition and had, later in life, discovered a specific set of tiles called Penrose tilings which are recognizable in floor designs in various buildings. Coxeter was an expert geometer who introduced Escher to many higher-level geometrical concepts. Escher himself was interested in topology, the study of surfaces, and tessellations, non-overlapping patterns. It’s unclear if Escher was aware of the study of recursion in mathematics, but his work shows some of the most interesting examples of it in the arts.

Fractals


The above Escher work, Circle Limit III, was published in 1959, a full 20 years before Benoit Mandelbrot, the creator of the Mandelbrot set, began to study fractals. One can see that the image has an origin of sorts in the very middle, where each fish is perfectly aligned with each other. Once we look further out, we see the pattern becoming more complex and more fish fitting in the same area until the very border of the circle has indistinguishable (but really infinite) repetitions of the same design. If we were to zoom in on one of these tiny designs, we’d see that they go on forever. This is the very essence of recursion and an apt example of a fractal.
Optical Illusions
Escher’s study of mathematics, geometry, and topology led him to a fascination with concepts like non-orientable surfaces, an example of which is the Mobius strip. Seemingly paradoxical constructs such as this are common in mathematics, where they defy a naive interpretation and need a bit of mental gymnastics. Escher’s later work focused on these optical illusions, exploiting the fallibility of human vision and the way we perceive perspectives.


Fin
Escher’s work has significance far past its aesthetic value. As an untrained mathematician, he explored some of the most sophisticated constructs in topology and geometry before they were properly understood. His work is unconventional, mind-boggling, and inspiring.Howdie stranger!
If you want to participate in our photoshop and photography contests, just:
LOGIN HERE or REGISTER FOR FREE
-
says:
-
says:
skimmed through this article.. No mention of D. Hofstadter’s “Gödel, Escher, and Bach” which is a 800 page masterpiece analyzing those three’s work. Pick it up if you really enjoyed this article!
( 2 years and 4767 days ago ) -
says:
one of my favorite artists along with Dali… Nice write up!
( 2 years and 4767 days ago ) -
says:
I based one of my chops on his art.
( 2 years and 4767 days ago ) -
says:
I like them all. I especially like “Recursion.” I thought it must have been very challenging to sketch.
( 2 years and 4763 days ago ) -
says:
Nice article – I like how you brought the info and pictures together and the work print gallery is entirely new to me – thanks for sharing!
( 2 years and 4745 days ago ) -
says:
If we were to zoom in on one of these tiny designs, we’d see that they go on forever. “so true”
( 2 years and 4274 days ago ) -
says:
It makes you wonder what would have happened if he had never met Penrose. Let’s face it, Escher’s art is pretty remarkable and even if there has been a long tradition of many kinds of surrealism his work still stands out for the sort of reasons you’ve mentioned. It is amazing how many different kinds of people get atracted to Escher. We kitted out a whole set of offices with framed Escher prints once and no matter how the trends come and go with other artists Escher is always trucking along there and probably always will. The challenge of his optical illusions will never go away.
( 2 years and 4253 days ago ) -
says:
this painting sucks
( 2 years and 3716 days ago )







Not to say that trained mathematicians might only be feigning an understanding of the concepts expressed by Escher…
But, by being able to create products that beautifully showcase these concepts, Escher showed that he had truly, deeply understood them.
( 2 years and 4768 days ago )